
농도 문제인데, 어떻게 푸는지 까먹어서 틀린 문제
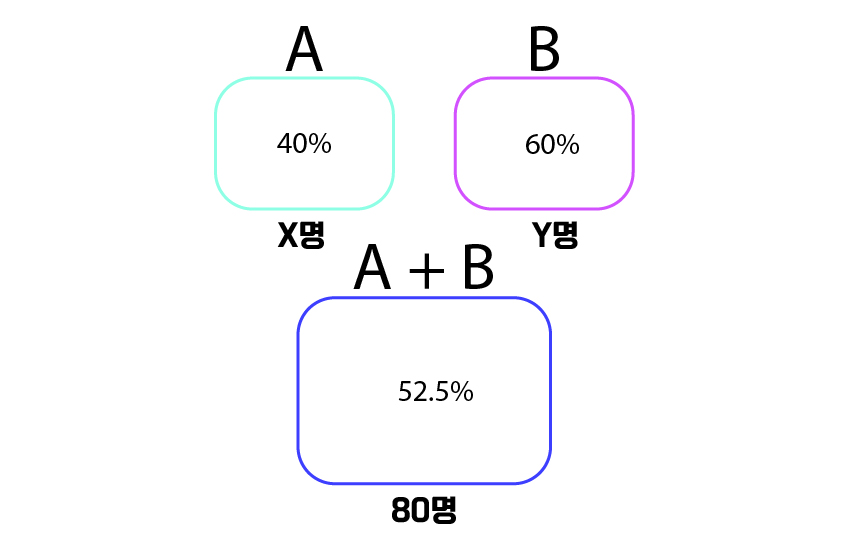
평균을 묻는 것인데 무슨 농도 문제냐고 할 수도 있다.
그러나 그냥 물이 있고, 소금이 있는 상황에서, 물이 몇 L 있고 소금이 몇 % 있느냐에 따라서 농도가 결정되는 것에 비추어 봤을 때, 결과적으로는 동일한 문제임을 알 수 있다.

A와 B의 평균 점수는 알지만 A와 B에 몇 명이 있는지는 모른다.
그렇지만
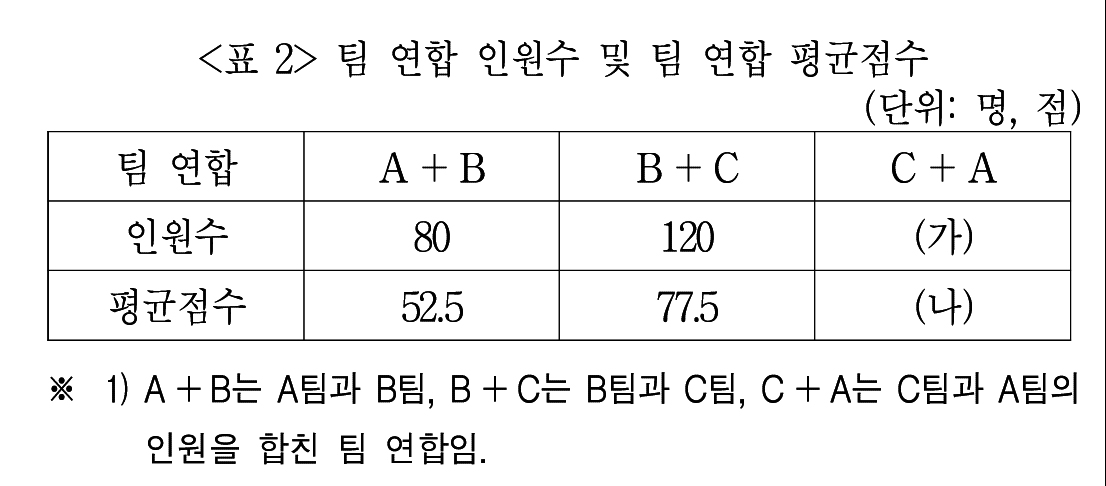
A와 B를 합친 인원은 80명이고 A+B의 평균점수는 52.5라는 것을 알 수 있다.
그래서 앞서 봤던 이런 구도라고 할 수 있다.

이걸로 뭘 할 수 있는지 이제 보자.

A의 평균 점수인 40%와 A+B의 평균 점수인 52.5%는 12.5%p 차이가 난다.
그리고
B의 평균 점수인 60%와 A+B의 평균 점수인 52.5%는 7.5%p 차이가 난다.
조금 건너 뛰어서 간단히 결론을 내면
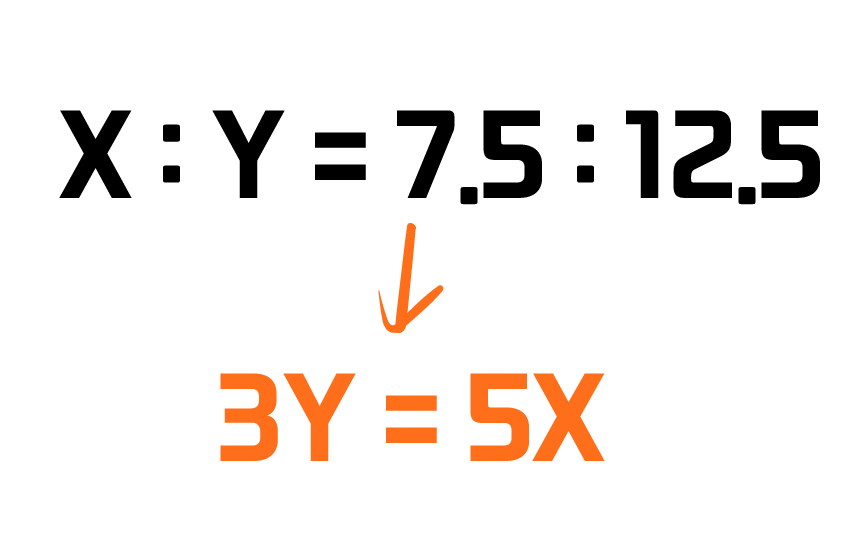
X와 Y의 관계는 위와 같게 된다.
그렇게 되는 이유
A+B의 평균 점수인 52.5%는 어떻게 계산 되었을까?

A인원들 점수 합과 B 인원들의 점수합을 A, B 전체 인원 수로 나눠줌으로써 구해진 것이다.
근데 A인원들 점수 합은 A 평균이 40%라는 것으로부터 구할 수 있는데,
평균 * 인원수를 하면 점수합이 나오는 것이다.
이는 B도 마찬가지여서
A 인원들 점수합은 0.4 * X
B 인원들 점수합은 0.6 * Y 가 되는 것이다.
그래서
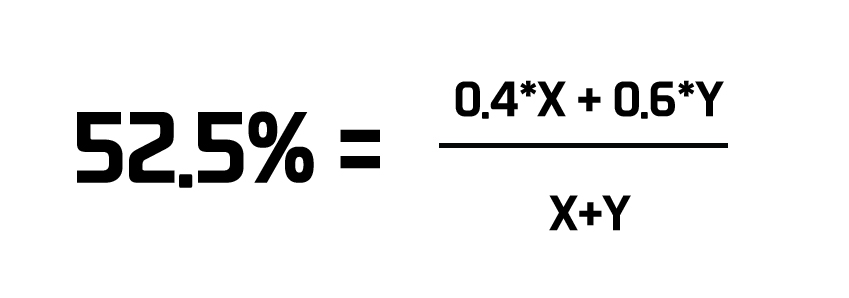
이런 식으로 다시 정리될 수 있다.
그러면

곱셈과 뺄셈을 하면 결과적으로
12.5 * X = 7.5 * Y 라는 것을 알 수 있는데,
이는

앞서 날로 먹는 식으로 보였던 것과 동일한 값을 보인다는 것을 알 수 있다.
아무튼, X + Y 값은 80이고, 3Y = 5X라는 것에 비추어 볼 때,
X = 30
Y = 50
임을 알 수 있다.

그렇다면 위 표에서 B + C의 인원수가 120이라는 것을 알고 있는 만큼,
C = 70이 된다.
그래서 C + A 인원수는 100이라는 것을 알 수 있다.

그리고 A와 C의 인원을 알았으니, A+C 의 평균점수를 구하는 건 매우 쉽다.

75%임을 알 수 있다.
그래서 답은 4번
'PSAT > 자료해석' 카테고리의 다른 글
| 2016년 민경채 PSAT 자료해석(5책형) 14번 오답 풀이 (4) | 2024.11.06 |
|---|---|
| 2017년 민경채 PSAT 자료해석(나) 25번 오답 풀이 (0) | 2024.11.05 |
| 2017년 민경채 PSAT 자료해석(나) 4번 오답 풀이 (0) | 2024.11.05 |
| 2017년 민경채 PSAT 자료해석(나) 14번 오답 풀이 (0) | 2024.11.05 |
| 2018년 민경채 PSAT 자료해석 25번 오답 풀이 (0) | 2024.10.30 |



