반응형

평균 문제

평균을 그냥 일일이 구할 필요는 없다.
까만 점은 1점
반점은 0.5점
빈 점은 0점
A를 보면 평균이 0.55다.
소수점을 제외하고 생각하면 55점이 된다.
그렇다면 까만 점은 평균보다 45점이 높고
반점은 -5만큼 낮다.
빈 점은 그렇다면 -55만큼 낮은 셈이다.
까만 점이 3개, 반점이 5개이므로
45*3 - 5*5 = 135-25 = 110
빈 칸이 2개 이므로 110/2 = 55
그러므로 0을 만들어 내기 위해서 두 빈 칸에는 빈 점이 들어가야 한다.

그렇다면 마찬가지 방법으로 나머지 빈 칸을 채워 넣을 수 있다.
B의 경우,
까만 점 4개
반점 4개
빈 점 1개
이므로
30*4-20*4-70 = 120-80-70 = -30
그렇기 때문에 -30을 0으로 만들려면 +30이 되어야 한다.
이는 까만 점 1개 이므로
B의 빈 칸에는 까만 점이 들어가야 한다.
그렇게 다 채워나가면
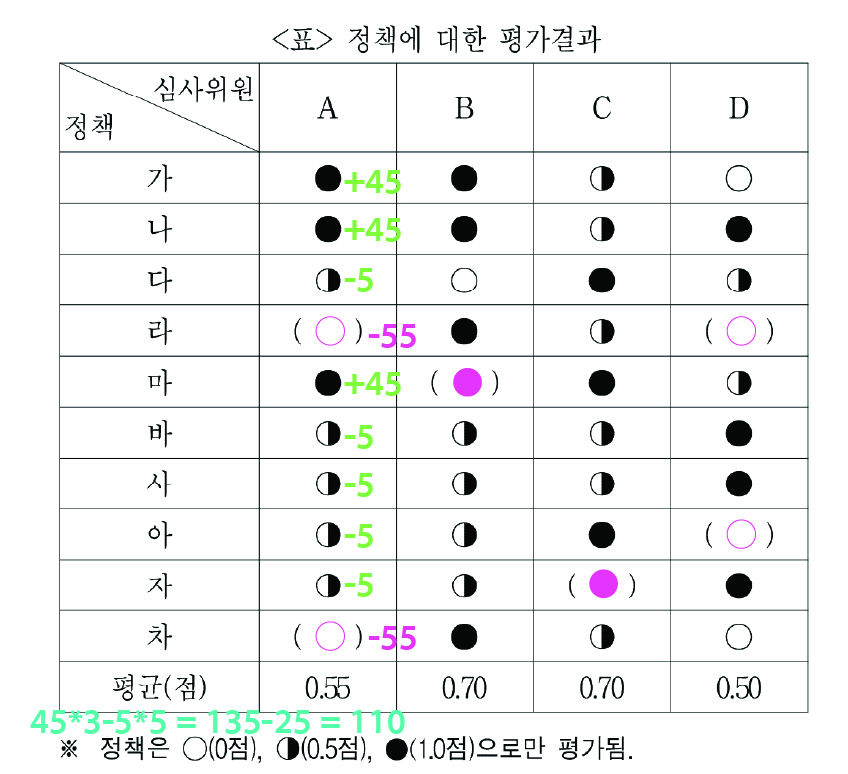
이런 결과가 나온다.
이제 총점이 가장 낮은 4개를 선정하면 된다.
딱 봤을 때, 0점이 2개인 '라'와 '차'가 가장 낮아 보인다.

그래서 답은 4번 아니면 5번이 된다.
4, 5번 모두 '아'를 포함하고 있으므로 차이점인
'다' 와 '자' 중에서 더 낮은 것을 선택하면 된다.

'다'는 2점
'자'는 3점
'다'가 더 낮으므로
답은 4번이 된다.
반응형
'PSAT > 자료해석' 카테고리의 다른 글
| 2016년 민경채 PSAT 자료해석(5책형) 14번 오답 풀이 (4) | 2024.11.06 |
|---|---|
| 2017년 민경채 PSAT 자료해석(나) 25번 오답 풀이 (0) | 2024.11.05 |
| 2017년 민경채 PSAT 자료해석(나) 4번 오답 풀이 (0) | 2024.11.05 |
| 2018년 민경채 PSAT 자료해석 25번 오답 풀이 (0) | 2024.10.30 |
| 2018 민경채 PSAT 자료해석 24번 오답 풀이 (1) | 2024.10.29 |



