
조건 확인하기

그렇다면 A에 반대하는 대표자는 3명일까?

이 조건에 의하면 A,B,C,D 네 개의 정책에 대해 찬성 혹은 반대 의견을 내야 함을 알 수 있다.
또한, 4개 정책에 모두 찬성한 대표자는 없고
4개 정책에 모두 반대한 대표자가 없음을 알 수 있다.
아무튼, 따라서 A에 반대하는 대표자는 3명이 된다.


그럼 일단 B에 찬성하는 대표자는 최소 2명이다.

그렇다면 B에 찬성하는 사람 총원은 짝수라는 것을 알 수 있다.

대표자는 총 5명이 있으므로
B에 찬성하는 대표자 수와
D에 찬성하는 대표자 수의 합은 5이하여야 한다는 것을 알 수 있다.
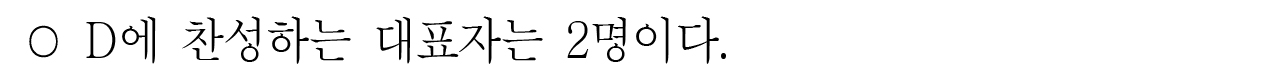
B에 찬성하는 대표자 수는 최소 2이고 D의 경우는 2다.
B에 찬성하는 대표자 수는 짝수여야 하므로
앞의 조건에 따라(B찬성 D찬성 합 = 5이하)
B에 찬성하는 사람 역시 2명이라는 것을 알 수 있다.
그럼 C에 찬성하는 대표자는 최소 1명
반대하는 대표자도 최소 1명이 되는 것임을 알 수 있다.


그렇다면 C에 찬성하는 대표자 수는 최소 1+2 = 3이 된다.
근데 4개 정책에 모두 찬성하는 대표자는 없으므로
딱 3명만이 C에 찬성한 것이 되고
그렇기 때문에 2명이 반대한 것이 된다.

이제 <보기>를 보자.
ㄱ. 최소여집합 느낌

이걸 어떻게 알 수 있을까?
A,B 찬성하는 대표자는 동일하다
따라서 반대하는 대표자도 동일하다.
일단 2개 정책에 반대하는 대표자가 3명 있다는 것은 알겠다.
C에 반대한 대표자 모두 A,B 찬성했던 대표자였을 가능성이 있지만
D에 반대한 대표자 모두 A, B 찬성했던 대표자였더라도 나머지 1명은 A, B에 반대했던 대표자가 포함될 수밖에 없다.
따라서 ㄱ. O
ㄴ.

이건 비교적 쉽게 알 수 있다.
ㄴ. O
ㄷ.

이것도 조건을 명확하게 이해했다면 비교적 쉽게 파악할 수 있다.
답: 5번
'PSAT > 언어논리' 카테고리의 다른 글
| 2022년 5급 언어논리 15번 오답 풀이 (1) | 2025.06.04 |
|---|---|
| 2021년 5급 언어논리 37번 오답풀이 (0) | 2025.06.02 |
| 2019년 5급 공채 PSAT 언어논리(가책형) 22번 오답 풀이 (0) | 2025.05.02 |
| 2019년 5급 공채 PSAT 언어논리(가책형) 17번 오답 풀이 (0) | 2025.05.02 |
| 2019년 5급 공채 PSAT 언어논리(가책형) 14번 오답 풀이 (0) | 2025.05.01 |



