
중요한 규칙
'가' 자리와 '나' 자리에는 사칙연산 부호 중 하나씩을 갑과 을이 각자 놀이에서 승리하기 위해 가장 유리한 대로 골라서 자신의 기록지에 적는다.
이를 통해 사칙연산 부호는 하나씩만 사용할 수 있다는 것을 알 수 있다.
(아래에 또 언급되어 있기는 하다. '한 사람이 같은 부호를 '가'와 '나'자리에 중복해서 쓸 수는 없다')
그리고 '가장 유리한 대로'라는 것은
승패의 결정은 점수가 더 높은 사람이 승리하는 것으로 한다. 다만 점수가 1점이 되면 상대가 아무리 높은 점수라 하더라도 1점이 되는 사람이 승리한다.
점수를 최대로 하거나, 1점이 되거나 둘 중 하나라는 것이다.
그래서 이제 선지를 보면
1번

일단 1을 만들 수 있는지 보자.
갑의 경우, 어떤 방법을 써도 1을 만들 수 없다.
그래서 점수를 최대로 만드는 것이 갑에게 가장 유리하다.
1+4*7 = 29점
을을 보면
5÷1÷5 = 1점을 만들 수 있을 것 같지만
사칙연산 부호는 하나밖에 사용할 수 없다.
그렇지만
5X1÷5 = 1점이 된다.
이러면 을이 무조건 이긴다.
1번. X
2번.
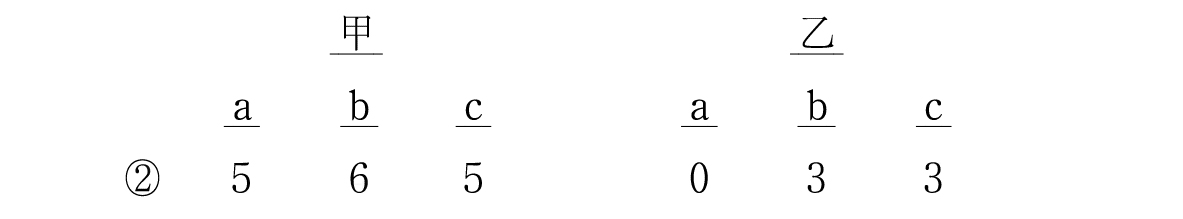
갑을 보면 1점을 만들 수 없는 것으로 보인다.
그렇지만 을은
0+3÷3 = 1점
이 되므로
을이 무조건 이긴다.
2번. X
3번.

갑을 보면
3÷(6-3) = 1
이렇게 되면 좋은데, 무조건 곱하기와 나눗셈을 먼저 해야 한다.
근데
3-6÷3 = 1이다.
을이 1점이 나올 수 없다면 갑이 무조건 이긴다.
을의 경우
1점을 만들 방법이 없다.
그러므로
갑이 무조건 우승한다.
3번. O
4번.

갑의 경우
3-3÷3 = 2점.
1점을 만들 수 없다.
그래서 최대로 하면
3X3+3 = 12가 된다.
을의 경우
1+6X2 =13점이므로
을이 이긴다.
4번. X
5번.

갑의 경우
1점이 나올 수 없다.
그래서 최대
4+5X7 = 39점
을의 경우
2-2÷2 = 1점이므로
을이 무조건 이긴다.
5번. X
답: 3번
'PSAT > 상황판단' 카테고리의 다른 글
| 2011년 5급 공채 PSAT 상황판단(선책형) 18번 오답 풀이 (0) | 2024.11.22 |
|---|---|
| 2011년 5급 공채 PSAT 상황판단(선책형) 17번 오답 풀이 (0) | 2024.11.22 |
| 2011년 5급 공채 PSAT 상황판단(선책형) 14번 오답 풀이 (0) | 2024.11.21 |
| 2011년 5급 공채 PSAT 상황판단(선책형) 13번 오답 풀이 (0) | 2024.11.20 |
| 2011년 5급 공채 PSAT 상황판단(선책형) 11번 오답 풀이 (1) | 2024.11.19 |



