
수식이 복잡해 보여서 그냥 패스한 문제

근데 역시나, 아니나 다를까, 이건 그냥 겁주기 용이었다.
일단 내용부터 이해하기
임의의 두 선수 X, Y의 엘로 점수를 각각 Ex Ey라 하고 X가 Y에게 승리할 확률을 Pxy, Y가 X에게 승리할 확률을 Pyx라고 하면, 각 선수가 승리할 확률은 다음 식과 같이 계산된다. 무승부는 고려하지 않으므로 두 선수가 승리할 확률의 합은 항상 1이 된다.
그래서 E는 엘로 점수고 P는 승리할 확률이다.
그런데 식을 보면

P를 계산하기 위해서는 E값을 알아야 하는 것으로 보인다.
이거는 공학용 계산기를 두드려야 풀 수 있는 문제로 느껴지기까지 한다.
그런데, 이어지는 내용을 보면
만약 한 선수가 다른 선수보다 엘로 점수가 200점 높다면, 그 선수가 승리할 확률은 약 0.76이 된다.
Ex-Ey든 Ey-Ex든 다 차이값이다.
엘로 점수가 200점 높다는 것은

이런 식으로 이해하면 된다.
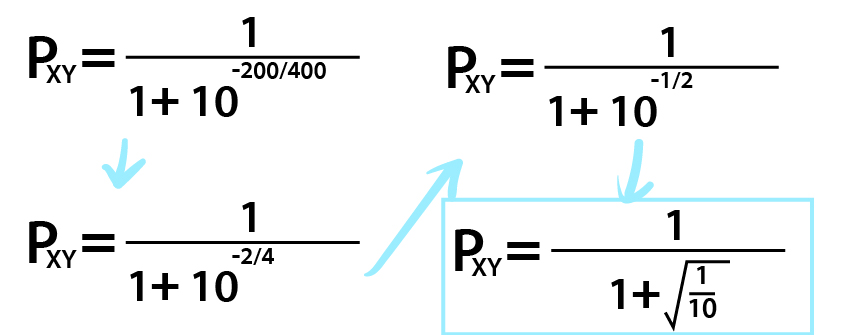
굳이 뭐 루트를 씌워가지 않아도 되는 것이다.
그리고 설령 이런 식으로 접근했다 한들, 이걸 머릿속에서는 풀기 어렵다.
그냥
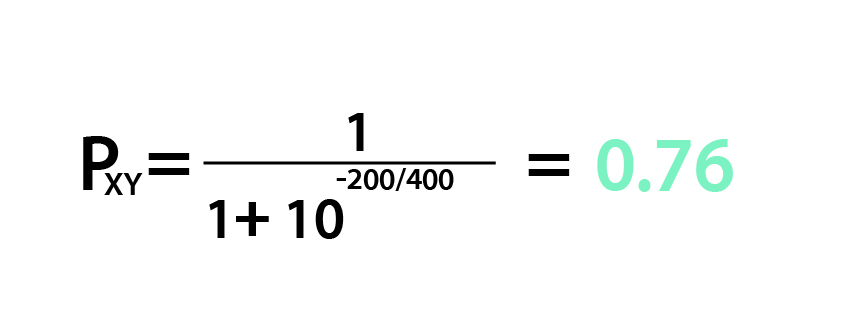
이렇다고 받아들이면 된다.
근데 하나 알 수 있는 건 있다.
만약에 엘로 점수의 차이가 200보다 커지거나 작아지면 어떻게 될까?
예를 들어, 차이가 0이 되거나 400 정도 차이가 나면?
일단 차이값이 0이 되는 경우는 앞서 나온 바 있다.
두 선수의 엘로 점수가 같다면, 각 선수가 승리할 확률은 0.5로 같다.
엘로 점수가 같다는 것은 차이값이 0이라는 것인데, 승리할 확률은 0.5가 된다고 한다.
그러면 여기서 알 수 있는 것은 엘로 점수 차이값이 높아질 수록 승리할 확률이 높다는 것이다.
이제 <보기>로 넘어가서,
ㄱ.
ㄱ. 경기에서 승리한 선수가 얻는 엘로 점수와 그 경기에서 패배한 선수가 잃는 엘로 점수는 다를 수 있다.
본문 마지막 문단을 보면 엘로 점수가 변화하는 방식을 알 수 있다.
경기에서 승리한 선수는 그 경기에서 패배할 확률에 K를 곱한 만큼 점수를 얻고, 경기에서 패배한 선수는 그 경기에서 승리할 확률에 K를 곱한 만큼 점수를 잃는다(K는 상수로, 보통 32를 사용한다).
X가 승리할 확률이 0.4고 Y가 승리할 확률이 0.6이라고 하면(왜냐하면 두 선수가 승리할 확률의 합은 항상 1이 된다고 했으니까)
X가 패배할 확률은 0.6, Y가 패배할 확률은 0.4가 된다.
X가 승리했고, Y가 패배했다고 하자.
그렇다면 X의 엘로 점수인 Ex는 32*0.6(패배할 확률)=19.2만큼 늘어나고,
Y의 엘로 점수는 32*0.6(승리할 확률)=19.2만큼 늘어난다.
그러니까, 한 선수가 얻는 점수와 다른 선수가 잃는 점수가 동일해진다.

한 선수가 승리할 확률은 다른 선수가 패배할 확률과 동일하고,
한 선수가 패배할 확률은 다른 선수가 승리할 확률과 동일하다.
그러니까 얻는 점수와 잃는 점수가 다를 수가 없는 것이다.
ㄱ.X
ㄴ.
ㄴ. K = 32라면, 한 경기에서 아무리 강한 상대에게 승리해도 얻을 수 있는 엘로 점수는 32점 이하이다.
아무리 강한 상대?
내가 마이크 타이슨과 맨 주먹으로 싸워서 이길 확률을 생각해 보자.
아마 승리할 확률은 0.00000000001도 안 될 것 같다.
그렇다면 패배할 확률은? 0.9999999999가 된다.
그렇다면 내가 승리했을 때 얻을 수 있는 엘로 점수는
32*0.999999999(패배할 확률)이다.
그런데, 0.99999999는 1에 근접하지만 1은 아니다. 그러니까
32*0.99999999 < 32이 된다.
근데, 패배할 확률이 100%라서 1이 된다고 해도
32*1 = 32다.
32보다는 클 수 없는 것이다.
ㄴ. O
ㄷ.
ㄷ. A가 B에게 패배할 확률이 0.1이라면, A와 B의 엘로 점수 차이는 400점 이상이다.
앞에서 봤던 식

이걸 떠올려 보자.
A가 B에게 패배할 확률이 0.1이라는 것은
반대로
A가 B에게 승리할 확률이 0.9라는 것이 된다.
엘로 점수 차이가 200이 될 때 0.76이었는데,
저기에 200 대신 400을 집어 넣으면?
일단 승리할 확률이 높아지긴 하겠는데, 0.9가 될지는 실제로 대입해 봐야 한다.
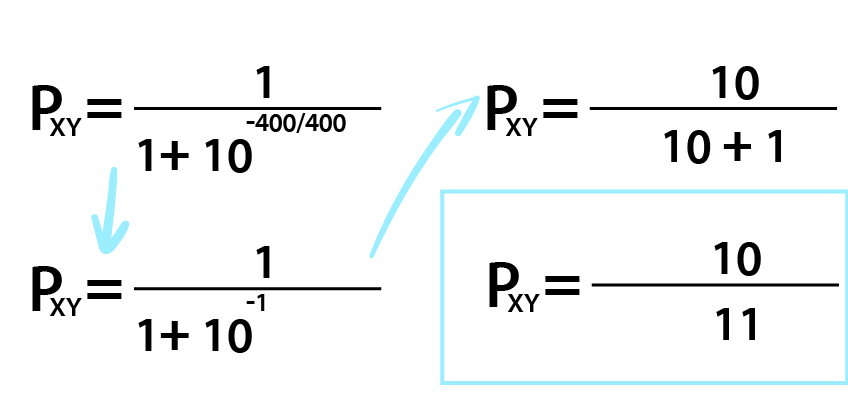
11분의 10이 되는 것이다. 이는 딱 봐도 0.9보다는 커 보인다.
그러니까 엘로 점수가 400 차이날 수가 없다는 것이다.
ㄷ. X
ㄹ.
ㄹ. A가 B에게 승리할 확률이 0.8, B가 C에게 승리할 확률이 0.8이라면, A가 C에게 승리할 확률은 0.9 이상이다.
일단,
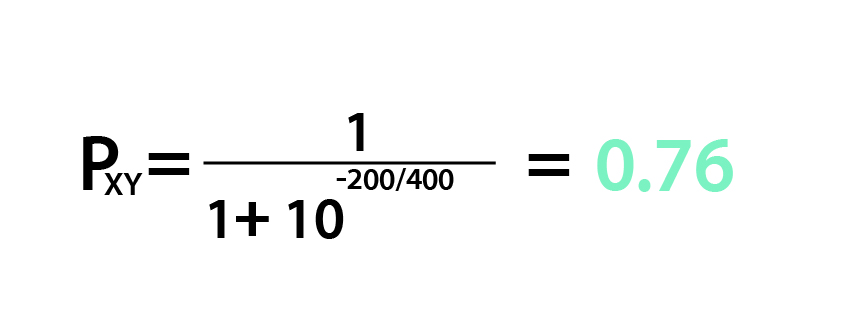
엘로 점수가 200 차이났을 때 승리할 확률은 0.76이다.
A가 B에게 승리할 확률이 0.8이기 때문에 엘로 점수 차이는 200보다 크겠지만
얼마나 차이나는지를 정확히 알려면 공학용 계산기를 두드려야 한다.
이는 당연히 불가능한 것이기 때문에 편의상 엘로 점수가 200 차이 난다고 가정해 보자.
B가 C에게 승리할 확률도 동일하게 0.8이라고 하니, 이 둘의 엘로 점수 차이도 200이라고 가정해 보자.
그렇다면 각자 엘로 점수 차이는 이렇게 된다.
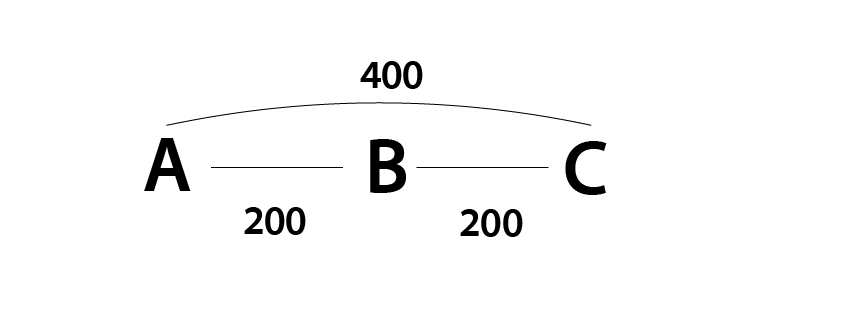
이를 통해 A와 C 간 엘로 점수 차이는 400이 된다는 것을 알 수 있다.
그렇지만 실제로는 400보다 더 크다.
차이가 400이라고 치면 ㄷ.에서 다뤘다시피,

승리할 확률은 11분의 10이 되는데, 이는 0.9보다 더 크다.
하물며, 엘로 점수 차이가 400보다 더 큰데, 승리할 확률은 11분의 10보다 더 크게 된다.
그러므로 A가 C를 상대로 해서 승리할 확률은 0.9보다 확실히 크다는 것을 알 수 있다.
ㄹ. O
답: 2번
'PSAT > 상황판단' 카테고리의 다른 글
| 2016년 민경채 PSAT 상황판단 7번 오답 풀이 (0) | 2024.11.05 |
|---|---|
| 2017년 민경채 PSAT 상황판단(나) 24번 풀이 (0) | 2024.11.04 |
| 2017년 민경채 PSAT 상황판단 25번 오답 풀이 (0) | 2024.11.02 |
| 2018년 민경채 PSAT 상황판단 25번 오답 풀이 (0) | 2024.10.28 |
| 2018년 민경채 PSAT 상황판단 21번 오답 풀이 (0) | 2024.10.26 |



