17번 - 최소여집합
<표2>를 보니 2인 공동 수상도 있고, 3인 공동 수상도 있는데,
이게 '연도별로 몇 명이다'로 주어진 게 아니고 전체적으로 주어진 상황에서
대체 공동 수상자 수를 어떻게 구할 수 있는지 고민하기만 했던 문제다.
근데, 공동 수상자가 있다면 단독 수상자도 있을 수 있다는 것을 간파하지 못했던 게 큰 문제였다.
2인 공동 수상자가 몇 명이냐, 3인 공동 수상자가 몇 명이냐에 집중한 나머지
전체 수상자에서 단독 수상자를 뺄 생각을 못해서 시간만 낭비한 문제라고 할 수 있다.
효율적으로 생각하자.
ㄱ.
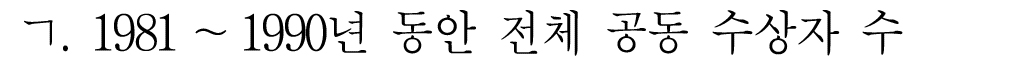
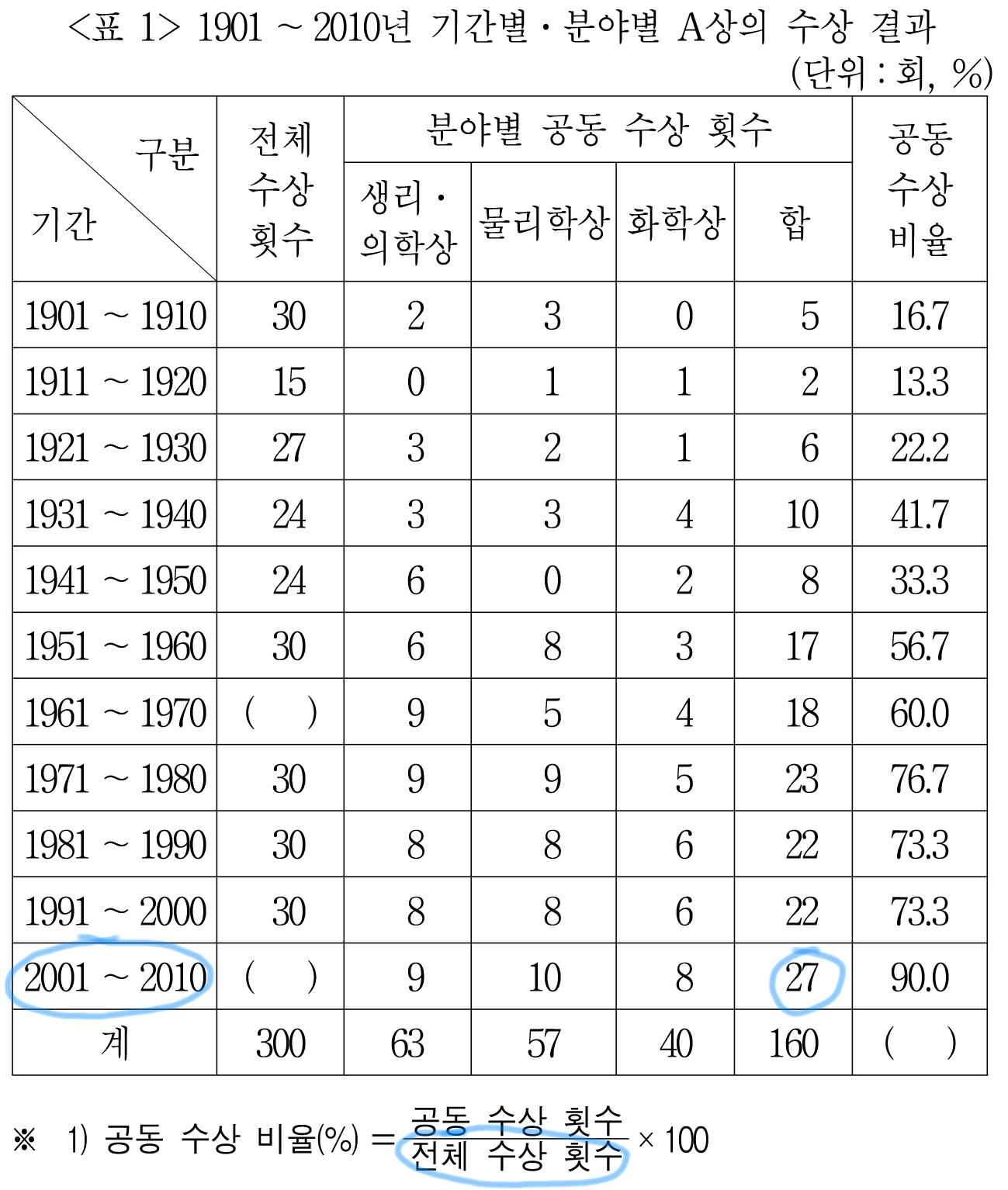
공동 수상 관련해서는 <표1>에서 확인할 수 있다.
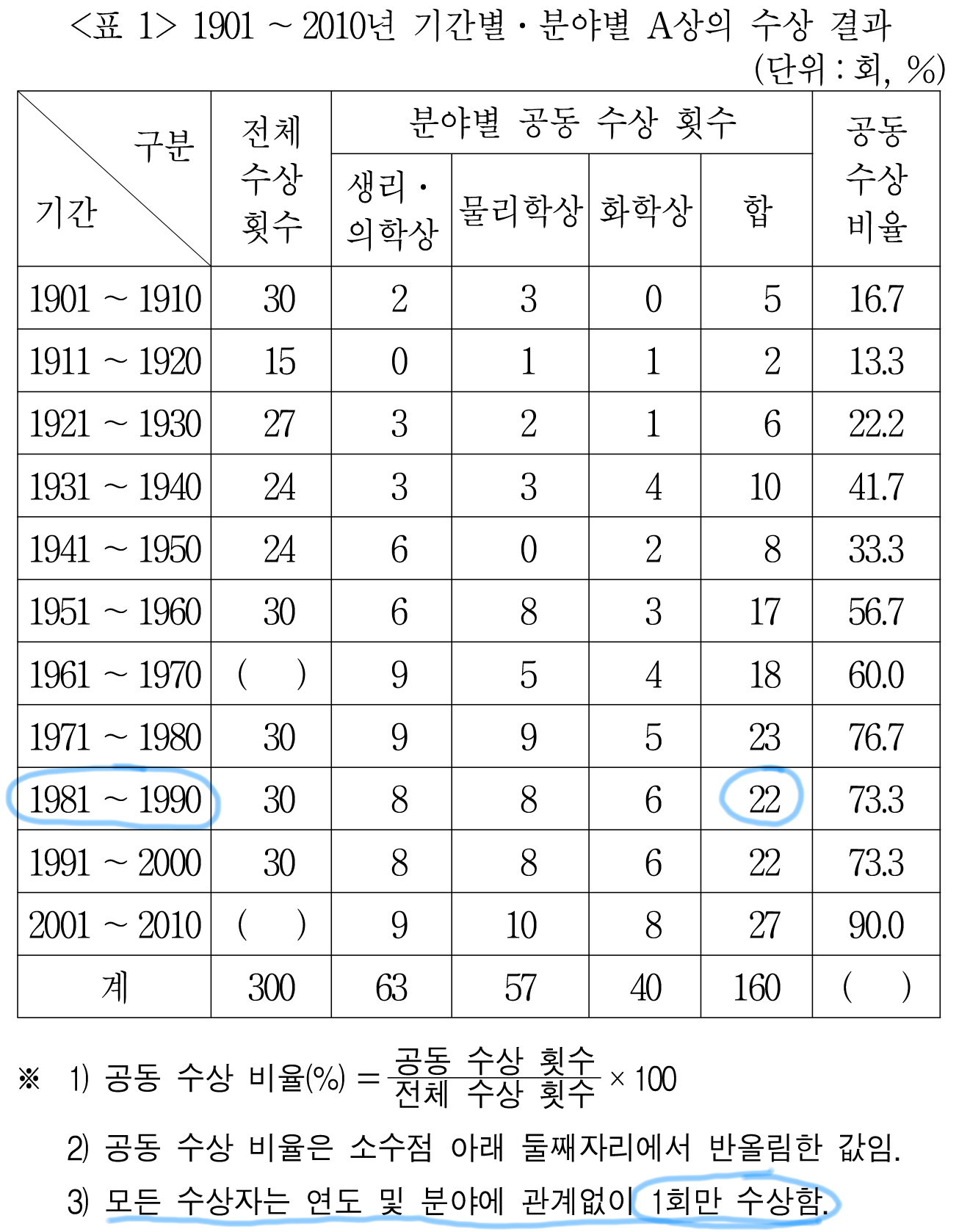
근데, <표3>을 보면

1981 - 1990 기간 동안 65명이 A상을 받았다고 한다.
그리고 <표2>를 보면

2인 공동 수상하고 3인 공동 수상이 있다는 것을 알 수 있다.
그러면 이 65명 중 몇 명이 2인 공동 수상을 했고, 몇 명이 3인 공동 수상을 했는지는 주어진 자료로는 찾을 수 없으므로
누가 공동 수상을 안 했는가를 찾기만 하면 된다.
다시 <표1>을 보면

전체 수상 횟수는 30회
공동 수상 횟수는 22회
그렇다면 공동 수상이 아닌 수상 횟수는 8회.
모든 수상자는 연도 및 분야에 관계 없이 1회만 수상한다고 했으므로
공동 수상이 아닌 단독 수상을 받은 사람은 8명이 된다.

그러면 65 - 8 = 57명이 된다.
ㄱ. 57
ㄴ.
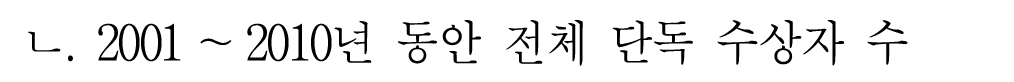
그럼 전체 수상 횟수 - 공동 수상 횟수를 구하면 되는 것인데,
전체 수상 횟수를 모른다.
근데 공식이 있다.
그래서 전체 수상 횟수 = 공동 수상 횟수/공동 수상 비율 이 된다.
그러면 27/0.9 = 270/9 = 30
즉, 전체 수상 횟수는 30이 되는 것이다.
30 - 27 = 3이므로
2001 - 2010 단독 수상자는 3명이 된다.
ㄴ. 3
ㄷ.

<표2>에서 확인 가능하다

전체 수상 횟수는 100
공동 수상 횟수는 57.
단독 수상자는 43명
2인 공동 수상 횟수가 29회이므로 29*2 = 60 -2 = 58
3인 공동 수상 횟수가 28*3 = 90 -2*3 = 84
43 + 58 + 84 = 185명
ㄷ. 185
답: 5번
18번

17번에서 멘붕와서 못 풀고 지나갔던 문제인데, 18번은 상대적으로 쉬운 문제라서 별 어려움 없이 풀 수 있다.
ㄱ.

<표2>를 봐야 한다.

생리 · 의학상 2인 공동 수상 횟수는 31.
생리 · 의학상 전체 수상 횟수는 100.
당연히 30% 넘는다.
ㄱ. O
ㄴ.

마찬가지로 <표2>를 보면

화학상 전체 수상 횟수는 100.
공동 수상 횟수는 40.
따라서 화학상 단독 수상자 수는 60명.
물리학상 전체 수상 횟수는 100.
공동 수상 횟수는 57
따라서 물리학상 단독 수상자 수는 43.
60이면 40의 1.5배인데,
43이면 1.5배보다 낮을 수밖에 없다.
ㄴ. X
이제 ㄷ. 만 맞는지 보면 된다.
ㄷ. 넘겨야 할 눈을 가지자

아 이거는 전체 수상자가 몇 명인지 구해야 한다.
넘어가고. ㄹ.을 보자
ㄹ.


1921 - 1930 기간에 단독 수상자 수는 21명
1941 - 1950 기간에 단독 수상자 수는 16명
5명 더 많은 게 맞다.
ㄹ. O
답: 3번
그럼 나머지 선지도 한번 보자
ㄷ.

이건 <표2>를 보면 된다.

생리 · 의학상 전체 수상자 수는
단독 수상자 37
2인 공동 수상자 31*2 = 62
3인 공동 수상자 32*3 = 96
37 + 62 + 96 =
37 + 62 + 100 -4 =
37 + 162 -4 =
197 -4 =
193
물리학상 전체 수상자 수는 17번에서 봤듯이,
185.
단독 수상자 수는 43
어? 지금 전체 수상자 수만 합해도 거의 400 가까이 되는데
단독 수상자 수는 37 + 43 = 80명밖에 안 된다.
화학상에서 단독 수상자 수가 120 이상 나오지 않는 이상 절대 50% 될 리가 없다.
근데, 화학상 단독 수상자 수는 간단히 구할 수 있는데,
60명에 불과하다.
그러므로 ㄷ. X
ㅁ.

2001 - 2010년 전체 단독 수상 횟수는 17번에서 봤듯이, 3명이다.
그리고 1901년 - 2010년 전체 단독 수상 횟수는

37 + 43 + 60 = 140.
100이어야 3이 3%되는 건데,
140이다. 당연히 3은 140의 3%가 될 리 없다.
ㅁ. O
'PSAT > 자료해석' 카테고리의 다른 글
| 2013년 5급 공채 PSAT 자료해석(인책형) 20번 오답 풀이 (0) | 2025.02.21 |
|---|---|
| 2013년 5급 공채 PSAT 자료해석(인책형) 19번 오답 풀이 (0) | 2025.02.21 |
| 2013년 5급 공채 PSAT 자료해석(인책형) 6번 오답 풀이 (0) | 2025.02.18 |
| 2012년 5급 공채 PSAT 자료해석(인책형) 31, 32번 오답 풀이 (0) | 2025.02.09 |
| 2012년 5급 공채 PSAT 자료해석(인책형) 27번 오답 풀이 (0) | 2025.02.08 |



