
경우의 수 + 확률이 조합된 문제
문제에서 갑이 선택할 수 있는 경우로는
1, 2
2, 3
3, 4
로, 총 3개다.
을의 경우는 1, 2, 3, 4 중에서 하나만 고르면 되기 때문에
1
2
3
4
총 4개의 경우가 존재한다.
그런데, 승패를 생각해 보면

전체 경우의 수를 생각해 보면
갑은
1, 2
2, 3
3, 4
중 하나를 선택할 수 있고, (3가지)
을은
1
2
3
4
중 하나를 선택할 수 있기 때문에 (4가지)
3*4 = 12가지 경우의 수가 존재한다.
갑이 우승하는 경우의 수는
갑이 1, 2를 선택했을 때 을이 3이나 4를 선택하는 경우 등이 있다.
갑이 선택할 수 있는 경우마다 우승할 수 있는 경우가 2가지 있는 셈이므로
3*2 = 6가지 경우의 수가 존재한다.
그렇기 때문에 갑이 이 게임에서 우승할 확률은 6/12 = 50%다.
이를 통해서 패배할 확률(즉, 을이 우승할 확률)도 50%라는 것을 알 수 있다.
을이 우승하는 경우의 수는
갑이 우승하는 경우의 수와 동일하게 생각해서,
을은 4가지를 선택할 수 있다.
각 경우마다 우승하기 위해서는
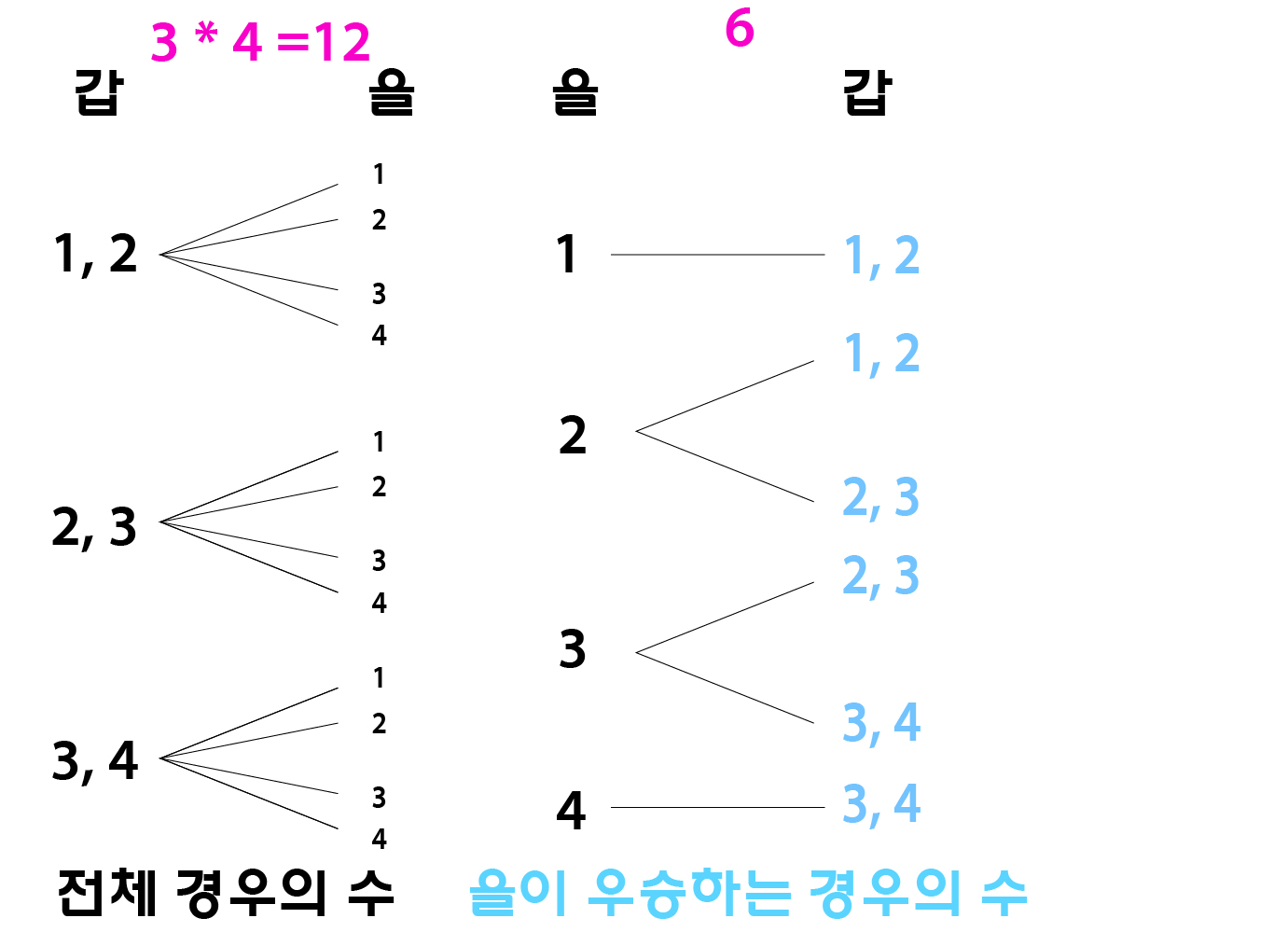
위와 같은 경우가 존재하는데, 6가지다.
그렇기 때문에 을이 우승할 확률도 6/12 = 50%다.
이제 <보기>를 보자
ㄱ.
괴물이 위치할 칸을 갑이 무작위로 정할 경우, 을은 1 보다는 2를 선택하는 것이 승리할 확률이 높다.

을이 1을 선택할 때 승리할 경우를 생각해 보면
6가지 경우의 수에서 하나 밖에 존재하지 않는다.
그렇기 때문에 확률은 1/6이다.
을이 2를 선택할 때 승리할 경우를 생각해 보면
6가지 경우의 수에서 2개가 존재 한다.
그렇기 때문에 확률은 2/6이다.
그래서 1보다는 2를 선택하는 것이 우승 확률이 높은 것이다.
ㄱ. O
ㄴ.
화살이 명중할 칸을 을이 무작위로 정할 경우 갑은 2, 3 보다는 3, 4를 선택하는 것이 승리할 확률이 높다.
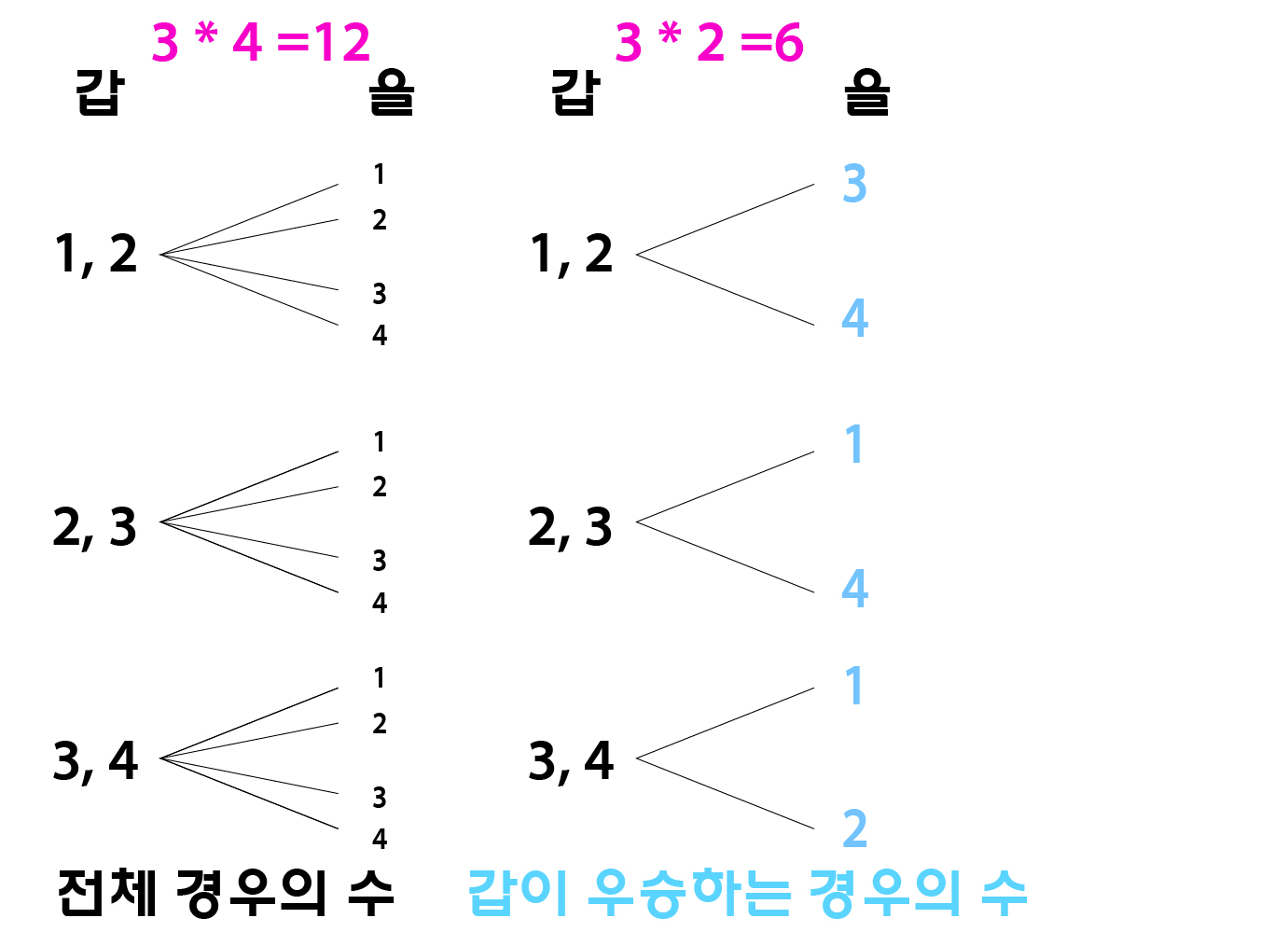
앞서 봤듯이, 2, 3을 선택해서 우승할 수 있는 경우의 수는 2개
3, 4를 선택해서 우승할 수 있는 경우의 수도 2개다.
갑이 우승할 수 있는 총 6가지 경우의 수에서 각각의 확률은
2/6 2/6으로 동일하다.
그래서 어니 하나가 다른 것보다 확률이 높다고 할 수 없다.
ㄴ. X
ㄷ.
이 게임에서 갑이 선택할 수 있는 대안은 3개이고, 을이 선택할 수 있는 대안은 4개이므로 을이 이기는 경우의 수가 더 많다.
그럴싸한 선택지인데, 틀렸다.
갑이 선택할 수 있는 대안이 3개이고, 을이 선택할 수 있는 대안이 4개인 건 맞는데,
각각 우승할 수 있는 경우의 수는 6개로 동일하다.
그렇기 때문에 ㄷ. X
답 : 1번
'PSAT > 상황판단' 카테고리의 다른 글
| 2015년 민경채 PSAT 상황판단(인책형) 24번 오답 풀이 (0) | 2024.11.07 |
|---|---|
| 2016년 민경채 PSAT 상황판단 24번 오답 풀이 (0) | 2024.11.05 |
| 2016년 민경채 PSAT 상황판단 7번 오답 풀이 (0) | 2024.11.05 |
| 2017년 민경채 PSAT 상황판단(나) 24번 풀이 (0) | 2024.11.04 |
| 2017년 민경채 PSAT 상황판단 25번 오답 풀이 (0) | 2024.11.02 |



