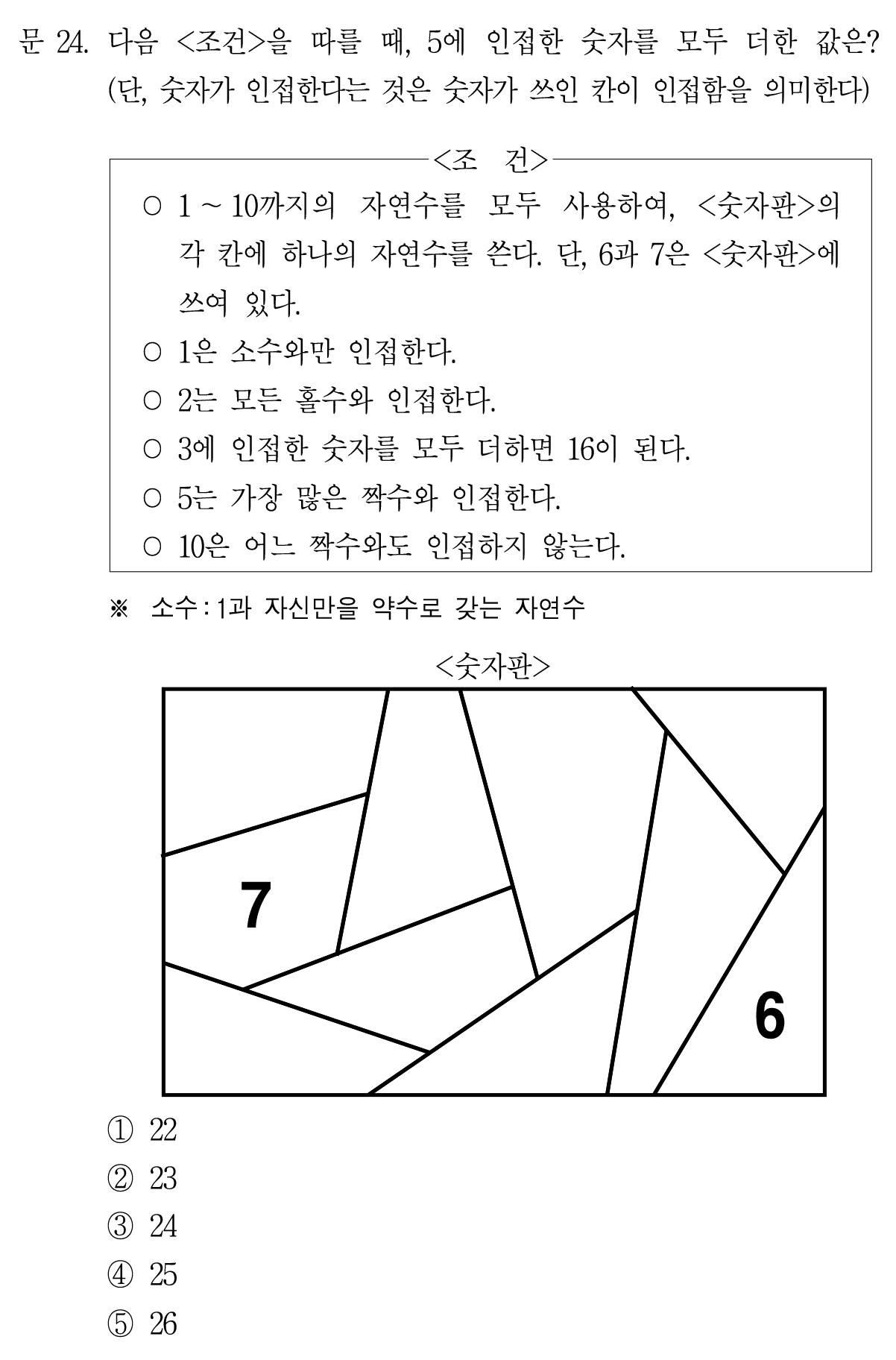
퍼즐을 맞추고 싶은데, 정보가 조금 부족하게 느껴져서 틀린 문제
1은 소수와만 인접한다.
그러니까 2, 3, 5, 7과만 인접한다는 것인데,
2, 3, 5, 7과 모두 인접한다고 한 적 없기 때문에 이 중에서 어느 것과 인접하는지는 모르겠다.
2는 모든 홀수와 인접한다.
2는 그러면 1, 3, 5, 7, 9와 인접하게 된다.
5개의 숫자와 인접할 수 있는 공간은

2로 표시한 두 공간 밖에 없다.
그런데, 모든 홀수와 접한다고 했으므로
2의 위치는
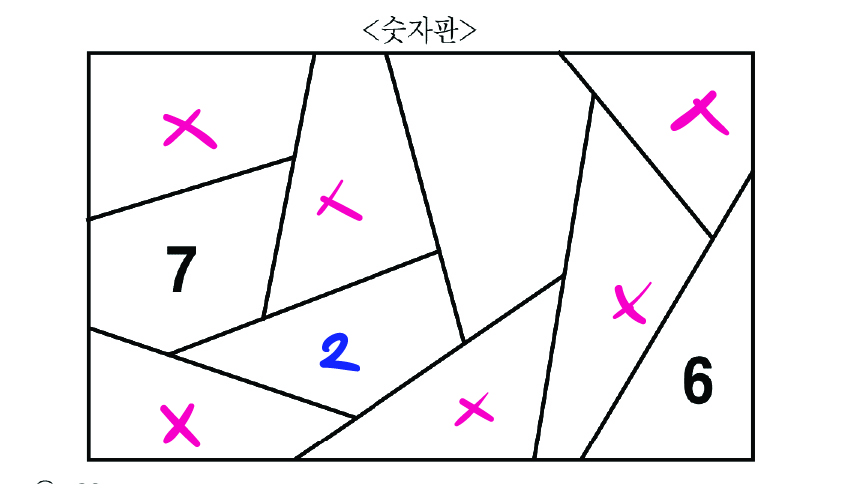
위와 같게 된다.
그리고
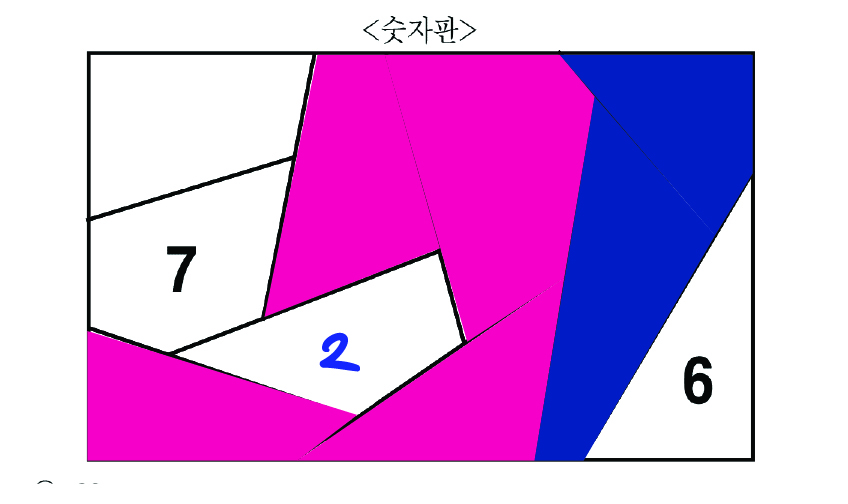
2는 모든 홀수와 인접하므로 분홍으로 칠해진 곳은 홀수만,
파란색으로 칠해진 곳은 짝수만 들어갈 수 있다.
3에 인접한 숫자를 모두 더하면 16이 된다.
16이라.
16이면
두 개의 숫자와 접한다면
10+6
9+7
이라는 두 경우가 있고
세 개의 숫자와 접한다면
9+1+5
8+2+6
7+4+5
등이 있다. 일단은 보류
5는 가장 많은 짝수와 인접한다.
가장 많은 짝수면
2, 4, 6, 8, 10 5개와 접할 수도 있지만
4개 이하로 접할 수도 있다.
10은 어느 짝수와도 인접하지 않는다
그렇다면 10의 위치는
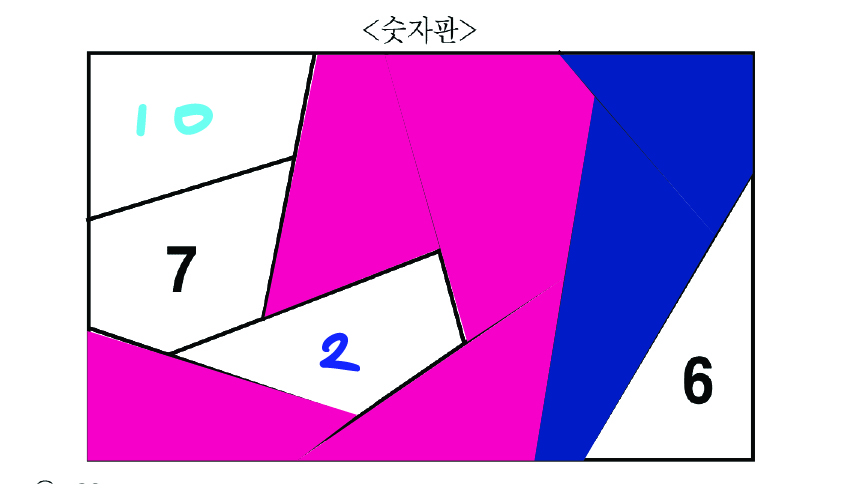
위와 같게 된다.
다시 1의 위치로 돌아가서,
1이 소수와만 인접한다고 했기 때문에
2와 10의 위치를 아는 시점에서 다시 확인해 볼 필요가 있다.
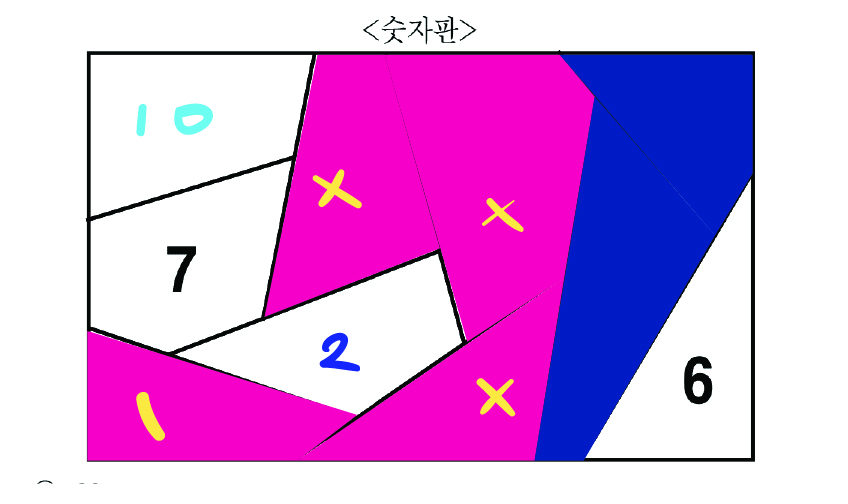
1이 있을 수 있는 위치는 위와 같다.
파란색에 있을 숫자는 4 아니면 8이고, 이는 소수에 해당하지 않기 때문에
파란색에 해당하는 칸과는 접하지 말아야 한다.
3이 있을 수 있는 위치는
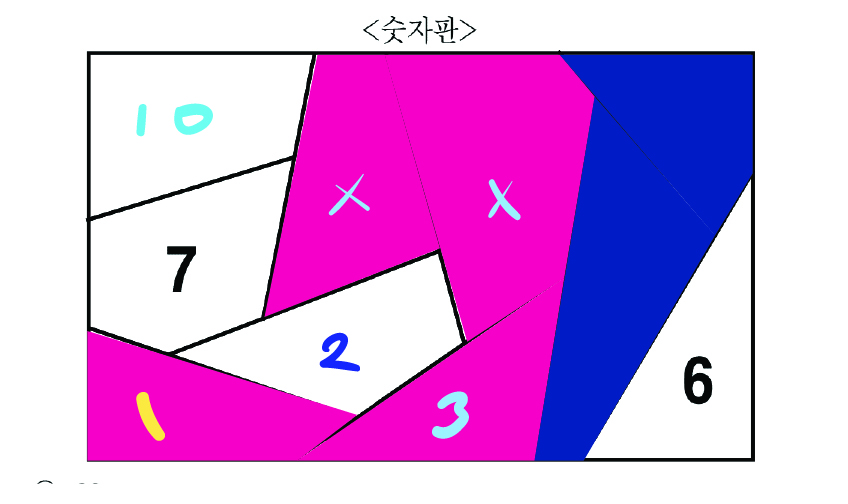
3에 인접한 숫자를 모두 더하면 16이라고 했으므로
2 바로 위 칸은 절대 될 수 없다. 벌써 10과 7이 있어서 16을 초과하기 때문이다.
그 옆칸의 경우에는 나머지 남은 짝수인 4와 8과 접하는데, 이를 더하면 벌써 12다.
거기에 2와도 접하기 때문에 또 더하면 14가 되는데,
16이 되려면 남은 두 칸이 각각 1이어야 한다.
그렇기 때문에 해당 위치에 3이 들어갈 수 없는 것이다.
5가 있을 수 있는 위치는

5는 가장 많은 짝수와 인접한다고 했다.
2 바로 위칸에 있으면 2와 10이 유일한 짝수지만
그 옆 칸에 위치하면 2와 4, 그리고 8이 있기 때문에 3개의 짝수와 인접할 수 있게 된다.
2보다는 3이 더 크므로 해당 위치에 있는 것이 맞다.
각 홀수의 위치를 알기 때문에 9가 어디에 있는지를 알 수 있다. 그렇지만 4와 8이 어디에 있는지는 불확실하다.

하지만 상관 없다.
어차피 5에 인접한 수를 모두 더하면 되기 때문이다.
그래서 9+2+3+4+8 = 26이 된다.
답: 5번
'PSAT > 상황판단' 카테고리의 다른 글
| 2015년 민경채 PSAT 상황판단 25번 오답 풀이 (0) | 2024.11.08 |
|---|---|
| 2015년 민경채 PSAT 상황판단(인책형) 24번 오답 풀이 (0) | 2024.11.07 |
| 2016 민경채 PSAT 상황판단 20번 오답풀이 (0) | 2024.11.05 |
| 2016년 민경채 PSAT 상황판단 7번 오답 풀이 (0) | 2024.11.05 |
| 2017년 민경채 PSAT 상황판단(나) 24번 풀이 (0) | 2024.11.04 |



