
지문 이해하기

항아리에 공이 몇 개 들어 있는지는 모른다.
근데 검정 공이거나 하얀 공이다.
첫번째 두번째 검정공이 나왔을 때
세번째로 검정공이 나올 확률이 어떻게 될지에 대해 설명할 예정이다.

일단 논리 요소만 고려한 '계산법 A'에 의하면
첫째, 둘째 공이 검정일 때 셋째 공이 검정일 확률은 1/2이라고 한다.
'논리적으로 생각해 볼 때 새로 꺼낼 공이 검정일 확률과 하양일 확률은 같다'에서
'엥? 아니 검정공이 몇 개 들어 있고 하양공이 몇 개 들어있는지도 모르는데 어떻게 같다고 하는 거지?'라고 생각했다.
근데 알았으면 이렇게 생각할 일도 없다.
검정공 1개 하양공 1개가 있다는 것을 알면
검정공 뽑을 확률은 1/2라는 건 다들 안다.
그러면 이런 접근 방식은 필요 없다.
그렇지만 모르기 때문에 이런 식으로 접근하는 것이다.
아무튼 '계산법 A'에서는
공이 검정공, 하양공으로 나뉘는 상황이기 때문에
결과는 검정으로 나올 수도 있고, 하양으로 나올 수도 있기 때문에 이런 맥락에서 1/2이라고 한 것이라고 이해해야 할 것 같다.
아무튼 여기까지가 '계산법 A'에 대한 내용이다.

그 다음으로 '계산법 B'에 대해 소개하고 있다.
경험 요소만을 고려한 계산인데,
3번 뽑았는데 3번 모두 검정이 나왔다면 4번째로 검정공이 나올 확률이 3/3이라는 것이다.
근데 4번째에서 하양공이 나왔다면
(근데 확률이 3/3이면 100%라는 얘긴데. 뭔가 여기서도 문제가 있는 듯 하다.)
3/4가 되는 것이다.

그리고 마지막으로 '계산법 C'인데,
'계산법 A'하고 '계산법 B'를 고려한 방안이다.
이제 문제를 풀어 보자.
19번

계산법 C에 대한 문제다. 잘못된 걸 골라야 한다.
1번

계산법 A에 의하면 검정공이 나올 확률과 하양공이 나올 확률은 1/2로 같다.
계산법 B에 의하면 첫째공이 검정공일 때 두번째로 검정공이 나올 확률은 1/1이다.
그러면 계산법 C에 의하면 두번째로 검정공이 나올 확률은
2/3이다.
그리고 검정공이 두번째에서 나왔다면 세번째로 검정공이 나올 확률은 지문에서 주어진대로
3/4다.
근데, 두번째에 검정공이 아니라 하양공이 나왔다면?
계산법 B에 의하면
1/2가 된다.
그렇다면 계산법 C에 의하면 이 경우에는
2/4가 된다.
그렇기 때문에 바로 직전에 나온 공의 색깔(검정/하양)은 이후에 꺼낼 공이 바로 그 색깔(검정)을 지닐 확률을 변화시킨다.
1번. X
2번

계속해서 검정공이 나오면 다음에 검정공이 나올 확률은

2/3, 3/4 4/5....계속 늘어난다.
근데, 검정공 대신 하양공이 나왔다면 그 다음에 검정공이 나올 확률은
2/3, 2/4가 된다.
그래서 증가와 감소를 반복할 수 있다.
2번. X
3번


이 식을 봐도 0도, 1도 되지 않는다는 것을 볼 수 있다.
3번. X
4번

1만번 했다고 해 보자.
그러면 분모에 2 더해지는 거,
분자에 1 더해지는 게 큰 의미가 있을까?
없다.
그렇기 때문에 계산법 B와 비슷해진다고 볼 수 있다.
4번. X
5번

그렇다면

으로 고칠 수 있다.
애초에 분자에 더해지는 것이 검정공이 나온 횟수인데,
검정공과 하양공이 나온 횟수가 동일하다면
전체 횟수의 절반한 것이 검정공이 나온 횟수와 동일하기 때문이다.
그래서 식을 변형하면

1/2이 됨을 알 수 있다.
그래서 5번. O
답: 5번
40번

ㄱ.

계산법 A는 1/2로 계속 동일하고,
계산법 B는 항아리 안에 검정공과 하양공이 동일한 비율로 주어져 있을 때 1/2에 근접한다.
검은 공과 하얀 공이 동일한 비율로 주어져 있다는 가정이 있으므로.
계산법 C도 N이 커질수록 계산법 B에 크게 영향을 받기 때문에 1/2에 근접한다고 볼 수 있다.
결국은 모두 비슷해진다.
ㄱ. O
ㄴ.

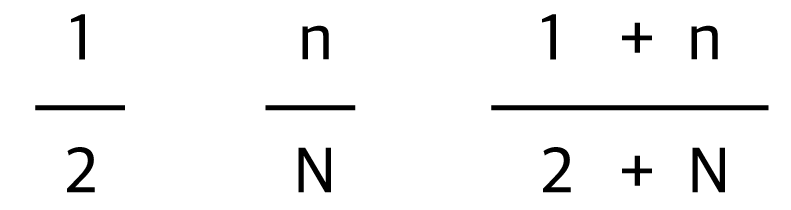
계산법 C가 계산법 A보다 클 수 있음은 이미 봤다.
그래서 계산법 C가 계산법 B에 비해 더 클 수 있는지 보자.

결론은 계산법 B로 인한 결과가 1/2보다 적을 때
계산법 C는 계산법 B보다 크다는 것을 알 수 있다.
그럼 계산법 B로 도출한 결과가 계산법 A보다 작다는 것인데,
이제 계산법 C가 계산법 A보다 큰 조건을 봐야 한다.

보니까 계산법 C가 계산법 A보다 크려면 계산법 B가 계산법 A보다 커야 한다.
근데 계산법 B가 계산법 A보다 크면 계산법 C는 계산법 B보다 작아지게 된다.
그러므로 ㄴ.X
ㄷ.

마찬가지로 부등호가 꼬이기 때문에
계산법 C가 가장 작지도 않다.
ㄷ. X
답: 1번
'PSAT > 언어논리' 카테고리의 다른 글
| 2013년 5급 공채 PSAT 언어논리(인책형) 31번 오답 풀이 (0) | 2025.02.13 |
|---|---|
| 2013년 5급 공채 PSAT 언어논리(인책형) 12번 오답 풀이 (0) | 2025.02.12 |
| 2012년 5급 공채 PSAT 언어논리(인책형) 35번 오답 풀이 (0) | 2025.01.25 |
| 2012년 5급 공채 PSAT 언어논리(인책형) 34번 오답 풀이 (0) | 2025.01.24 |
| 2012년 5급 공채 PSAT 언어논리(인책형) 33번 오답 풀이 (0) | 2025.01.22 |



